浮点数表示法#
与科学计数法相似,任意 \(J\) 进制数 \(N\),总可以写成:
式中 \(M\) 称为数 \(N\) 的 尾数 (mantissa),是一个纯小数;\(E\) 为数 \(N\) 的 阶码 (exponent),是一个整数,\(J\) 称为缩放因子 \(J^E\) 的底数。这种表示方法相当于数的小数点位置随缩放因子的不同而在一定范围内可以自由浮动,所以称为 浮点表示法。
底数是事先约定好的(常取 2),在计算机中不出现。在机器中表示一个浮点数时,一是要给出尾数,用定点小数形式表示。尾数部分给出有效数字的位数,因而决定了浮点数的表示精度。二是要给出阶码,用整数形式表示,阶码指明小数点在数据中的位置,因而决定了浮点数的表示范围。浮点数也要有符号位。因此一个机器浮点数应当由阶码和尾数及其符号位组成:
其中 \(E_s\) 是阶符(表示阶码的符号),\(E_1 E_2 \cdots E_n\) 的阶码,\(M_s\) 是尾符(数 \(N\) 的符号),\(M_1 M_2 \cdots M_n\) 的尾数。
当底数取 2 时,二进制数 \(N\) 的小数点每右移一位,阶码减小 \(1\),相应尾数右移一位;反之,小数点每左移一位,阶码加 \(1\),相应尾数左移一位。
为了提高数据的表示精度,当尾数的值不为 \(0\) 时,其绝对值应大于等于 \(0.5\),即尾数域的最高有效位应为 \(1\),否则要以修改阶码同时左右移小数点的方法,使其变成这一要求的表示形式,这称为 浮点数的规格化表示。
当浮点数的尾数为 \(0\) 时,不论其阶码为何值,或者当阶码的值遇到比它能表示的最小值还小时,不管其尾数为何值,计算机都把该浮点数看成 \(0\) 值,称为 机器零。
浮点数所表示的范围比定点数大。假设机器中的数由 \(8\) 位二进制数表示(包括符号位):在定点机中这 \(8\) 位全部用来表示有效数字(包括符号);在浮点机中若阶符、阶码占 \(3\) 位,尾符、尾数占 \(5\) 位,在此情况下,若只考虑正数值,定点机小数表示的数的范围是 \(0.0000000\) 到 \(0.1111111\),相当于十进制数的 \(0\) 到 \(127 /128\),而浮点机所能表示的数的范围则是 \(2^{-11} \times 0.0001\) 到 \(2^{11} \times 0.1111\),相当于十进制数的 \(1/128\) 到 \(7.5\)。显然,都用 \(8\) 位,浮点机能表示的数的范围比定点机大得多。
备注
IEEE 754 浮点数计数标准,可以表示为:
因此,只要给出:符号(\(S\))、阶码部分(\(E\))、尾数部分(\(M\)) 这三个维度的信息,一个浮点数的表示就完全确定下来了,所以 float 和 double 这两种类型的浮点数在计算机中的存储结构就表示成下图所示这个样子:
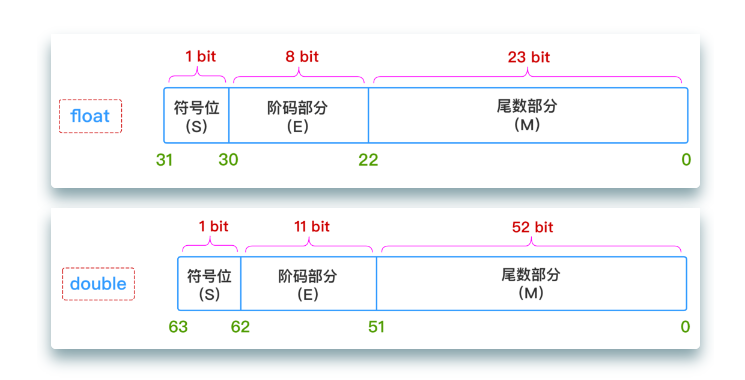
对于 float 型浮点数,指数部分 \(8\) 位,考虑可正可负,因此可以表示的指数范围为 \([-127, 128]\);
对于 double 型浮点数,指数部分 \(11\) 位,考虑可正可负,因此可以表示的指数范围为 \([-1023, 1024]\)。
浮点数的精度是由尾数的位数来决定的:
对于 float 型浮点数,尾数部分 \(23\) 位,换算成十进制就是 \(2^{23}=8388608\),所以十进制精度只有 \(6 ~ 7\) 位;
对于 double 型浮点数,尾数部分 \(52\) 位,换算成十进制就是 \(2^{52} = 4503599627370496\),所以十进制精度只有 \(15 ~ 16\) 位。
所以,浮点数交给计算机存储的时候,可能会有精度丢失问题!
在指令集(Instruction Set Architecture)的内置数据类型中,定点数是整数,浮点是二进制格式。一般来说,指令集层面的定点是连续的,因为它是整数,且两个邻近的可表示数字的间隙是 \(1\)。另一方面,浮点代表实数,其数值间隙由指数确定,因而具有非常宽的值域(32 位数值最大整数是 \(2^{31}-1\),而浮点值域为 \(2 - 2^{-23} \times 2^{127}\),值越接近零就越准确。在给定指数时,浮点在不同范围内拥有数值数量相同数量。
